[AA-part1] Parallel architectures

Course: https://ucilnica.fri.uni-lj.si/course/view.php?id=89
Lecturer: prof. dr. Dušan Kodek
Language: English, Slovenian
Date: 2014-02-24

Lecturers (3 parts):

1. prof. dr. Dušan Kodek - Parallel architectures, SIMD, MIMD
2. prof. dr. Borut Robič - Parallel algorithms, PRAM
3. doc. dr. Tomaž Dobravec - CUDA architecture, OpenCL

The purpose of this course is to introduce students to the field of parallel computing which is in many areas becoming a basic tool for problem solving. The topics include architectures of parallel computers as well as algorithms that are needed for this type of computation and are closely related to a given architecture. The structure of the course will allow students to use theoretical knowledge for the practical design of parallel computer systems and parallel algorithms that can be used for complex problem solving. The latest parallel computers will be studied as examples and the advanced tools for solving a typical parallel problem will be given.

Course overview (part 1):

• limitations of serial computation: IPC, Tomasulo algorithm, superscalar and VLIW approach
• development of parallel architectures and technology: vector, SIMD and MIMD
• interprocessor communication problems and interconnect networks
• review of architectures used in the most powerful parallel computers to date

Exams depend on the lecturers, are more individual, and you contact them when you are ready. Basic structure:

1. homework (seminar or written exam at home)
2. oral exam

Kontaktna oseba za litraturo (dve mapi) je as. A. Božiček. Oglasit pri prof. D. Kodeku, da dobiš domačo nalogo, ki jo je potrebno rešiti pred ustnim izpitom.

Introduction

Reasons for parallel computation

Transistors/chip: 1971 ~ \(10^4 / \text{chip}\) .. 2014 ~ \(10^{10} / \text{chip}\); ~1000000x more

Clock frequency (speed/transistor): 1971 ~ \(1 \text{MHz}\) .. 2014 ~ \(5 \text{GHz}\); ~5000x more

Chip size/speed: ~200x more

Number of transistors per chip doubles every 18 months.

Amdahl’s law represents a limit on speedup.

We really have no choice.

Flynn classification (M. J. Flynn, 1966)

+-----------+ <--(instructions, m_I)---- +--------+
| Processor |                            | Memory |
+-----------+ <--(data/operands, m_D)--> +--------+

1. SISD (single instruction single data): \(m_I = 1\), \(m_D = 1\)
2. SIMD (single instruction multiple data): \(m_I = 1\), \(m_D = N > 1\)
3. MISD doesn’t exist
4. MIMD (multiple instruction multiple data, multicomputers): \(m_I = M \gg 1\) (thousands), \(m_D = N \gg 1\)

Types of parallelism:

1. Instruction parallelism (difficult because threads need to be identified before parallelization)
2. Data/operand parallelism

In list of Top500 supercomputers Tianhe-2 is the current top.

Enormous heat problem on each switch of transistor, each wire works as a resistor (heat energy = \(C * U^2 / 2\)). Voltage is decreasing from \(5 \text{V}\), \(3 \text{V}\), …, \(0.75 \text{V}\), but silicon transistors do not work bellow this. Power and heat give an upper limit on how big a processor can be.

Limitations of parallelism

Amdahl’s law (G. M. Amdahl, 1967):

\[ S(N) = \frac{1}{f + (1 - f) / N} \]

\(N\) .. number of processors
\(S(N)\) .. speedup
\(f\) .. sequential part
\(1 - f\) .. parallel part

Eg.: \(f = 0.1 \rightarrow S(N) \leq 10\); \(f = 0.001 \rightarrow S(N) \leq 1000\)

Parallelization is not universal, it is good for some problems, but not for all problems (eg. simplex algorithm is difficult to parallelize).

SISD computers

Where is the problem?

• pipeline, \(CPI \geq 1\) (clocks per instruction close to 1)
• pipeline hazards:
  1. data hazard (unavailable operands):
     • read after write (RAW) (flow dependence)
     • write after write (WAW) (antidependence)
     • write after read (WAR) (output dependence)
  2. control hazard (branch instructions)
  3. stuctural hazard (busy functional units)

Elimination of data hazards

FDIV F0, F5, F6  ; F0<-F5/F6
FADD F4, F0, F2
FSUB F8, F2, F1

Register F0: RAW hazard (~1960) is a true data hazard and nothing can be done, except dynamic execution (reordering of instructions).

FDIV F0, F5, F6
FADD F4, F0, F2
FST 0(R1), F4
FSUB F2, F3, F7
FMUL F4, F3, F2

Register F2: WAR (antidependency)

Register F4: WAW (output dependency)

WAW and WAR hazards represent naming dependencies that can be solved by renaming registers (F2\(\rightarrow\)FT1, F4\(\rightarrow\)FT2):

FDIV F0, F5, F6
FADD FT2, F0, F2
FST 0(R1), FT2
FSUB FT1, F3, F7
FMUL F4, F3, FT1

Who should do this renaming?

• programmer or compiler (software): same programs use many more registers, program can not adapt to newer processors with more registers
• hardware solutions (should solve in \(1\) instruction per \(0.145 \text{ns}\)):
  • scoreboarding (1963, CDC 6600)
  • Tomasulo algorithm (1967, IBM 360/91)

Tomasulo algorithm

(Chapter 7 in Kodek book.)

Recall that all processors (except simple) consist of multiple functional units (*, %, +/-, store, load) (sequential and parallel) that can also be pipelined or not. Each functional unit has a reservation station (FIFO or different). Waiting instructions IR are placed in one of the reservation stations if they are available (otherwise it waits) with either real or virtual values (until real values are available instruction is not executed).

Each reservation station has 6 parameters:

• \(O_p\) - operation to perform, each unit may have more operations
• \(U_j\), \(U_k\) - addresses of the reservation station that will produce results (for those that are waiting)
• \(V_j\), \(V_k\) - real values of 2 input operands/results
• \(R_j\), \(R_k\) - flags indicating when \(V_j\) and \(V_k\) are ready
• \(B\) - busy flag indicates reservation station (if all are busy there is a structural hazard and the instruction must wait)

Output from the functional unit is placed on common data bus (CDB) and goes back to all reservation stations that check if they need the resulting value (format, value, \(U_j\), \(U_k\)). The result also must also be written to programmer accessible registers of the architecture.

Implicit renaming is done at the issue stage when instructions are written into reservation stations. This resolved WAW and WAR hazards.

Processing stalls if the number of reservation stations for a functional unit is not high enough (or in case of jump instructions), but this rarely happens. Newer Intel processors have 50-60 places in reservation stations. The results get out in a different order, but renaming writes correct values.

What happens if there is a branch (jump)?

In this version everything stops and waits for it to complete. Improvement of Tomasulo’s algorithm allows speculative execution of instructions.

Speculation consists of:

• branch prediction
• speculative execution using a reorder buffer
• once the branch is resolved:
  1. correct prediction: ok
  2. wrong prediction: remove results of speculative execution from reorder buffer

Implementation is done by adding a reorder buffer (FIFO queue) to Tomasulo’s algorithm, working with it instead of directly with programmer accessible registers, and commit results in order instructions were given. But even with this we still have \(CPI \geq 1\). Newer computers (starting with Pentium Pro) use superscalarity (multiple-issue) and are capable of going to \(CPI \approx 0.5\).

Ponovitev

Date: 2014-03-03

Za redke probleme primerna velika paralelnost: napovedovanje vremena, kemijske reakcije, analiza dogajanja pri atomskih eksplozijah…

Pohitritev SISD:

• Tomasulov algoritem
• špekulativno izvrševanje ukazov z ROB (preureditveni izravnalnik)

Še vedno pa je: \(CPI \geq 1\), \(IPC = \frac{1}{CPI}\)

Večizvršitveni računalniki

Želimo doseči \(IPC > 1\) brez spreminjanja programov.

Poznamo pristopa:

• superskalarni procesorji
• VLIW/EPIC procesorji (dolgi ukazi)

Primer:

• \(n\)-izstavitveni procesor
• \(x_i = f(x_j, x_n)\)
• medsebojna odvisnost operandov (RAW, WAR, WAW)

Potrebno število kontrolnih primerjav:

\(1\). ukaz \(0\) primerjav
\(2\). ukaz \(2\) primerjavi
\(3\). ukaz \(2*2\) primerjav
\(n\). ukaz \((n-1)*2\) primerjav

Skupaj: \(2 * \sum_{i=1}^{n-1} i = 2 * \frac{(n-1)*n}{2} = n^2 - n\) primerjav

1. Superskalarni procesorji: strojno ugotavljanja/odpravljanje medsebojnih odvisnosti:

   procesor, leto, prevzem - izstavi - izvrši, funkcijskih enot
   IBM RS/6000, 1990, 2-2-2, 2
   Pentium Pro, 1995, 3-3-3, 5
   DEC Alpha, 1998, 4-4-11, 6
   Pentium 4, 2000, 3-3-4, 7
   Core 7, 2009, 6-6-4, 15, 30 primerjalnikov

2. VLIW procesorji (very long instruction word) (EPIC je kratica pri Intel Itanium): dolgi ukazi s fiksnim številom običajnih ukazov, ki se lahko izvršujejo paralelno

   Gre za programsko ugotavljanje/odpravljanje medsebojnih odvisnosti, kjer prevajalnik ugotovi kako razporediti (sprememba arhitekture zahteva recompileanje). Predvsem uspešno pri signalnih procesorjih, drugje nerodno.

Omejitve paralelizma na nivoju ukazov

Če je res, da lahko povečamo zmogljivost tako, da povečujemo število hkrati izstavljenih ukazov, se pojavi vprašanje koliko je sploh možno, če omejitev ne bi bilo?

Zamislimo si idealen superskalarni procesor:

1. neomejeno število registrov
2. vse napovedi skokov so pravilne
3. nobenih zgrešitev v predpomnilnikih

Kakšen je \(IPC\)? Na množici programov SPEC92:

• na idealnem: od 17.9 do 150 (povprečje \(\approx 80\))
• na \(n = 50\): od 80 do 45
• 3% napaka pri napovedi skokov: od 45 do 23
• pri 256 registrih: od 23 do 16
• resnični procesorji imajo IPC: od 2 do 4

Proizvajalci ne povečujejo \(IPC\) (kar bi profesionalni uporabniki želeli), ampak dodajajo več jeder (cores). To je lažje, pri marketingu hitrost preprosto pomnožijo, proizvajalci zmagali bitko za \(IPC\)…

Paralelnost na nivoju niti

Nit (thread) je zaporedje ukazov in pripadajočih operandov, ki se lahko izvršuje neodvisno od ostalih niti.

Programer je tisti, ki mora identificirati niti in poskrbeti za njihovo sinhronizacijo. Npr. diskretna Furierjeva transformacija, množenje matrik, seštevanje…

Vektorski računalniki (SISD)

Spadajo pod SISD, ne SIMD. Čeprav je en ukaz, se operacije izvedejo zaporedno.

\[ a(i) = b(i) + c(i), i=1..N \]

Pri njih izkoriščamo podatkovno (operandno) paralelnost. Prednosti:

1. elementi vektorja so skoraj vedno medseboj neodvisni (ni operandnih nevarnosti)
2. en vektorski ukaz pomeni \(N\) operacij –> manj ukazov (Flynnovo ozko grlo se odpravi)
3. veliko manj kontrolnih nevarnosti pri skokih (manj zank)
4. dostop do pomnilnika je regularen –> pomnilniško prepletanje je učinkovito

Ozko grlo prenosa podatkov med CPE in pomnilnikom se rešuje s širšim vodilom in s pomnilniškim prepletanjem (\(m\) modulov (npr. 16, 32, 64, 128, 256)).

Najbolj znana serija Cray (Cray 1, Cray X-M2…), ki so bili najhitrejši računalniki do začetka ~90-ih let. Te serije so imele sledeče funkcijske enote za operacije v plavajoči vejici (fiksna vejica ni relevantna):

1. +/-, 6
2. *, 7
3. 1/x, 17
4. load, 9 do 17
5. store, 9 do 17
6. gather/scatter, 6

Zgradba:

• vsak program ima skalarni in vektorski del
• vektorski registri (\(N = 64, 128, 256\)) (nariše kot škatla z dvojno črto zgoraj in spodaj)
• skalarni registri (nariše kot škatla)
• vektorska funkcijska enota (more znati po vrsti jemati iz vektorskega registra, na vsakem izvesti operacijo in pisati nazaj v vektorski register po vrsti) (narišemo kot valj s črtami)
• vektorska load/store enota
• VL (vector length) register (je vhodni podatek vsem fukcijskim enotam, dolžina 1 je identično skalarnemu, a počasnejša)

Primer DAxPy double-precision (64-bit); SAxPy single-precision (32-bit) z \(N = 64\):

\[ \vec{y} = a * \vec{x} + \vec{y} \]

Program na skalarnem računalniku:

LD F0, a
ADDI R4, Rx, #64
LD F2, 0(Rx)      :loop
MULTD F2, F0, F2
LD F4, 0(Ry)
ADDD F4, F2, F4
SD 0(Ry), F4
ADDI Rx, Rx, #1
ADDI Ry, Ry, #1
SUB R5, R4, Rx
BNZ R5, loop

(\(2+9*64 = 578\) ukazov, \(578\) urinih period)

Program na vektorskem računalniku:

LD F0, a
LV V1, Rx         ; V1<-x
MULSU V2, F0, V1  ; V2<-F0*V1
LV V3, Ry         ; V3<-y
ADDV V4, V3, V2   ; V4<-V3+V2
SV Ry, V4

(\(6\) ukazov, \(1+12+7+6+12+63 = 101\) urinih period)

Chaining: Procesor lahko začne izračun takoj, ko je en element operacije že naložen. Ni potrebno čakati, da se vektorski register do konca napolni. Med tem, ko se prvi shranjuje se en kasnejši še bere, a kljub temu ponavadi ne pride do težav.

Strip mining: Če imamo preveč podatkov, resnični vektor predstavimo kot mnogokratnik vektorjev dolžine \(64\).

Problem pogojno izvršljivih ukazov

Fortran koda:

    do 100 i=1,64
      if(A(i) ne 0) then A(i) = A(i) - B(i)
100 continue

Izvajanje na vektorskem računalniku:

LV V1, Ra        ; V1<-A
LV V2, Rb        ; V2<-B
LD F0, #0        ; F0<-0
SNESV F0, V1     ; VM<-1 if V1(i)!=0 else 0; scalar not equal vector
SUBV V1, V1, V2
CUM              ; VM<-1 v vsa mesta
SV Ra, V1        ; A<-V1

VM register (64-bitni mask), \(N=64\), \(\{N-1,N-2,...,0\}\)

Problem pri redkih matrikah (\(\vec{K}\), \(\vec{M}\) indeksna vektorja). Fortran koda:

    do 100 i=1,64
      A(K(i)) = A(K(i)) + C(M(i))
100 continue

Izvajanje na vektorskem računalniku:

LV V1, Rk        ; V1<-K
LVI V2, (Ra+V1)  ; V2<-A(K), gather
LV V3, Rm
LVI V4, (Rc+V3)  ; V4<-C(M)
ADDV V5, V2, V4
SVI (Ra+V1), V5  ; pomn<-A(K), scatter

Redukcija vektorjev

Date: 2014-03-10

    dot = 0
    do 10 i=1,64
10  dot = dot + A(i) * B(i)

Problema se ne da vektorizirat, če ne uporabimo trika za redukcijo vektorjev:

    do 10 i=1,64
10  Y(i) = A(i) * B(i)  ; vektorski ukaz
    dot = Y(1)          ; skalarni ukaz
    do 20 i=2,64
20  dot = dot + Y(i)    ; vektorski ukaz

Parametri za učinkovitost vektorskega računalnika (za primerjavo):

1. \(N_\inf\) - GFLOPS, teoretična zmogljivost, ki predpostavlja, da so vsi vektorji neskončno dolgi in vse funkcijske enote znajo delati z njimi
2. \(N_{1/2}\) - dolžina vektorja pri kateri se doseže \(N_\inf / 2\)
3. \(N_v\) - dolžina vektorja pri kateri postane vektorsko računanje hitrejše od skalarnega

Npr. družina Cray kjer ista funkcijska enota za skalarne in vektorske ukaze:

| $N_v = 2$, pri vektorskem ukazu je potrebno na začetku dolžino prenesti v funkcijsko enoto

Zakaj niso PC-ji vektorski?

| Dandanes sicer SSE, vektorski.
| Pri vektorskih se izkorišča operandno paralelnost.
| Zakaj imajo vsi PC-ji enoto za operacije v plavajoči vejici, čeprav samo 10% programov uporablja. Nekoč koprocesor (<486), cenovno tako ugodnejše.
| Razlog: cena CPE (registri so dragi), dostop do pomnilnika (širše prenosne poti, DRAM za skalarne dovolj)

GPU so postali popularni za GPGPU, a težko programirati, alternativa pa je Xeon Phi, ki ima 61-procesorjev in so programsko združljivi. Bomo videli kaj bo prevladalo.

Družina Cray:

| 1976  Cray-1
| ...
| 1996  Cray T90
| 2006  NEC
| MIMD  vektorski

Gordon Bell Prize (nagrada za računalnik, ki rešuje resničen problem, običajno manj kot polovica teoretične) - realne hitrosti:

| 1988  Cray Y-MP                    1 GFLOPS  zadnjič vektorski
| 1990  CM-2                        14 GFLOPS  zadnjič SIMD
| 2000  Grape-6                   1349 GFLOPS  MIMD
| 2010  Cray XP Jaguar            2330 TFLOPS  MIMD
| 2013  IBM Sequoia (BlueGene/Q)  14.4 PFLOPS  MIMD
| en core sodobnega PC teoretično 10

SIMD računalniki

Operandna/podatkovna paralelnost, ki jo je veliko lažje izkoriščati kot ukazno, saj programer že z definiranjem podatkovnih tipov omogoči izkoriščanje. Pri SIMD se ukazi v resnici izvedejo naenkrat, ne zaporedno kot pri vektorskih.

Vsi procesorji (imamo maskiranje) izvedejo isti ukaz na \(n\) operandih naenkrat. Imamo gosteči računalnik, ki se ukvarja z vhodom in izhodom, saj nima smisla, da se SIMD specializiran za računanje ukvarja s tem.

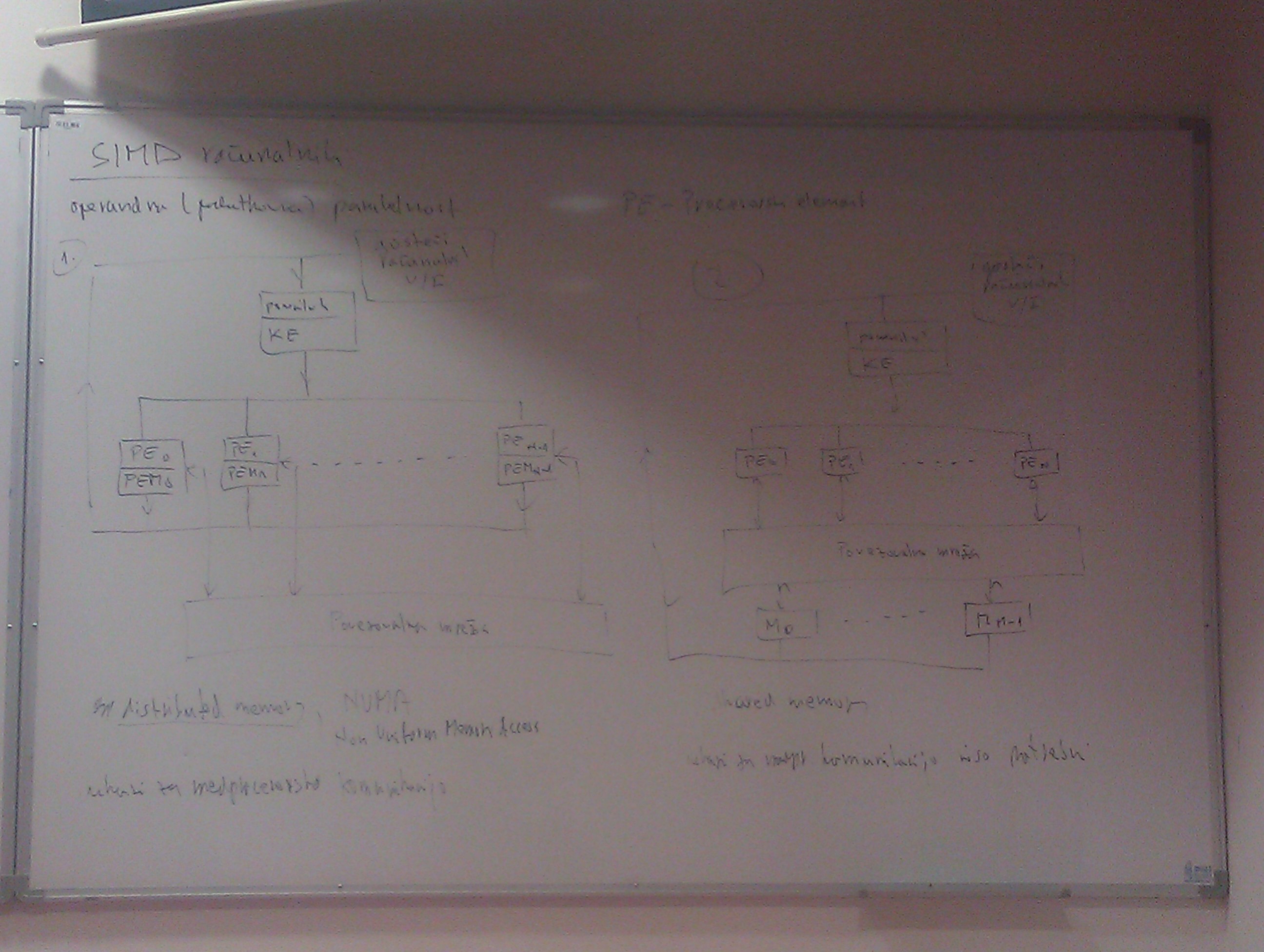
PE_i - Procesorski element/procesor
PEM_i - Pomnilnik procesorske enote, ki vrača vrednosti nazaj v pomnilnik ali gosteči računalnik (za V/I)
Povezovalna mreža za komunikacijo med PE

Dva tipa:

• distributed memory: povezovalna mreža za direktno komunikacijo med PE (posebni ukazi, čas dostopa krajši), NUMA - non-uniform memory access (čas glede na naslov ni enak)
• shared memory: povezovalna mreža je povezana med PE_i in M_i ter se obnaša isto kot pomnilnik, ukazi za medprocesorsko komunikacijo niso potrebni

Večina jih je prvega tipa, saj je dostopanje do namenske povezovalne mreže hitrejše (podobno kot pomnilniška hierarhija).

Povezovalne mreže

Obstajajo problemi kjer je medprocesorske komunikacije malo (npr. računanje DFT), a na žalost niso vsi taki. Problem je kako narediti takšno komunikacijsko mrežo kjer lahko vsak komunicira z vsakim hitro.

\[ R_i -> R_{f(i)}, i=0,1,...,n-1 \]

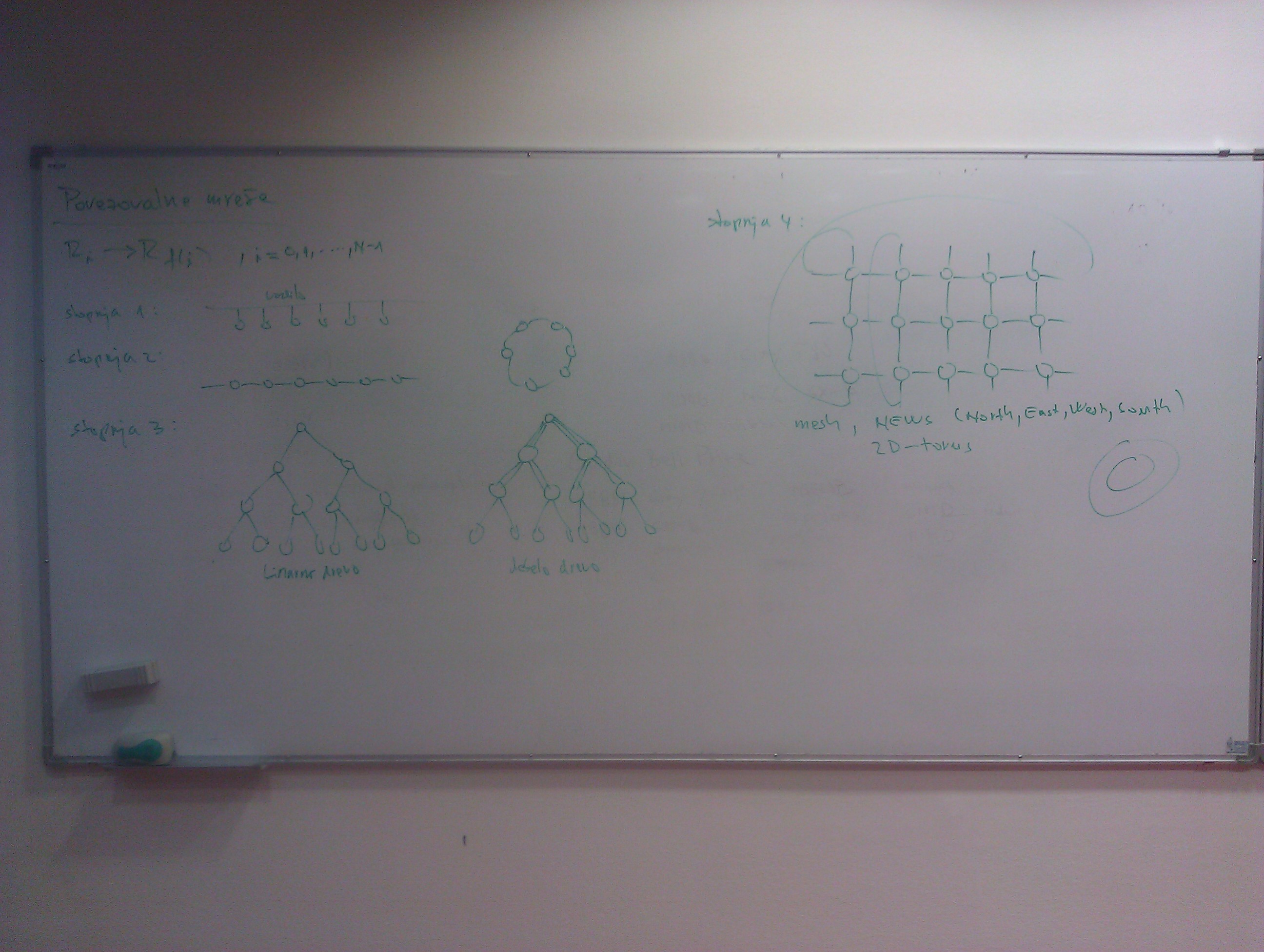
Stopnja 1: vodilo/bus, problem le en lahko naenkrat komunicira z enim

Stopnja 2: pot ali cikel, vsak povezan s sosednjima, problem so konfliktni dostopi, kjer je potrebno dostopati

Stopnja 3: binarno drevo, problem pri komunikaciji med skrajnima listoma; izboljšava je debelo drevo, kjer imamo v višjih vejah/deblu po več povezav s čimer zmanjšamo verjetnost konfliktov

Stopnja 4: mreža/mesh, NEWS (north-east-west-south), 2D torus (avtomobilska guma, če še zunanje povežemo), vsako vozlišče povezano s 4 sosedi, pri komunikaciji med procesorji je linerana zveza skozi koliko vozlišč mora informacija potovati

Stopnja 4 je postala popularna, ker je povezana z naravo velikega števila problemov (npr. vreme, potovanje vode), kjer se prostor razdeli na posamezne dele in noben dogodek ne deluje na daljavo ne da bi šel čez vmesne dele. Obstajajo pa tudi problemi matematične narave, kjer ni teh omejitev.

Stopnja 5: 3D torus, kot več NEWS ravnin ena nad drugo, vsako vozlišče povezano s 6 sosedi

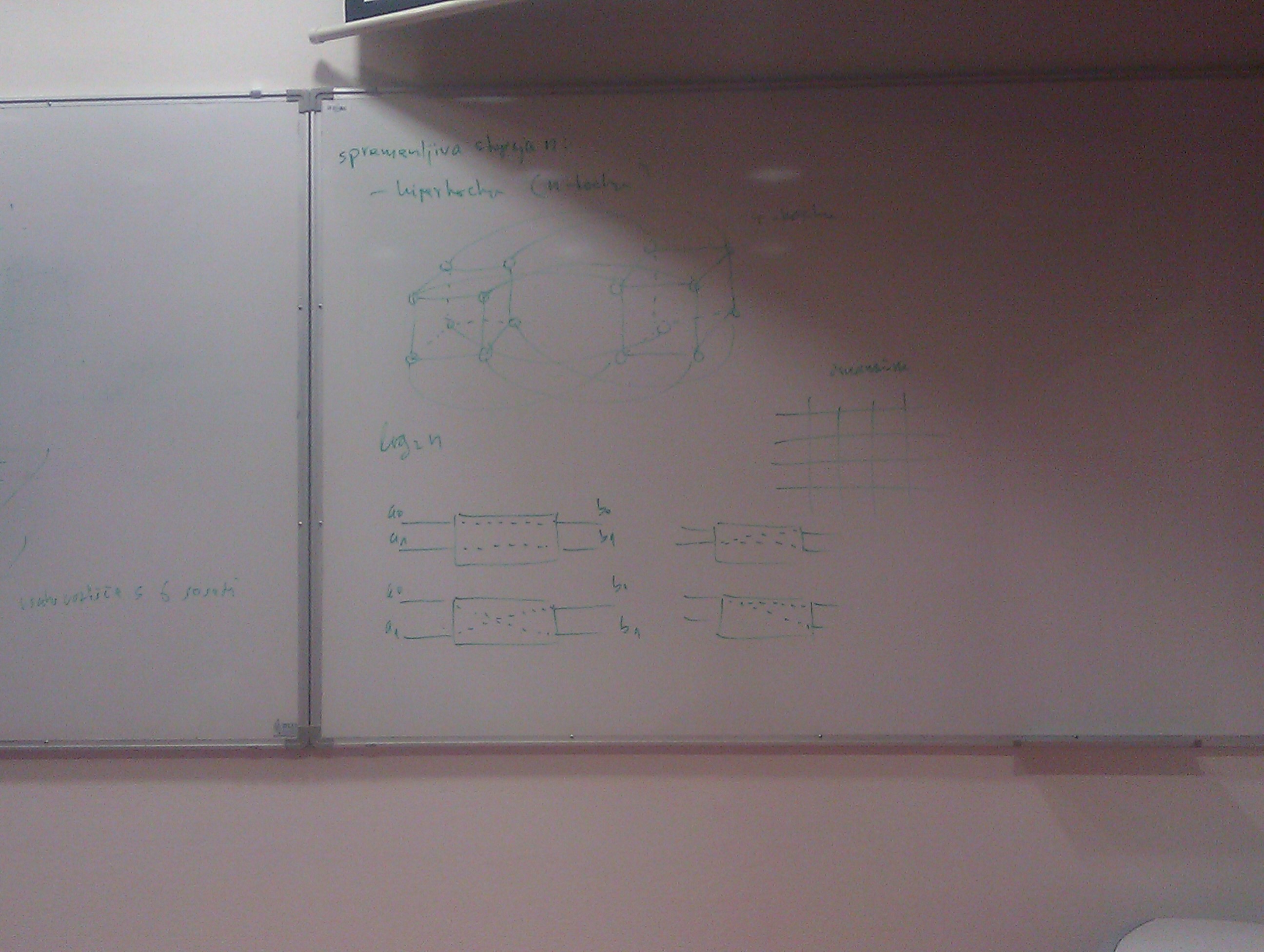
Spremenljiva stopnja \(n\):

• hiperkocka (\(n\)-kocka): število vozlišč skozi katere more iti sporočilo je \(log_2 n\), ni veliko takšnih (npr. Connection Machine 2)

To so bile statične mreže, obstajajo pa tudi dinamične mreže, kjer imamo stikala in se lahko povežejo po svoje. Pri Butterfly lahko sestavimo poljubno mrežo, če imamo stikalo, ki je sposobno potezati na oba načina.

Zgled: Illiac 4

Illiac 4 (1966-1972) izdelovali na Uni. Illinois, podjetje Westinghouse. Nekateri obtožujejo ta računalnik, da je upočasnil razvoj paralelnih računalnikov.

• cilj bil doseči 1000 MFLOPS (32-bitnih)
• 4 kvadrante s po 64 PE/kvadrant
• realizirali le 1 kvadrant
• kontrolna enota brez pomnilnika, 64 PE s PEM, gostujoči PC B6500
• problem feritni pomnilnik, stroški ogromni (porabili 4x več)

Hitrosti operacij:

+/- 350ns
* 450ns
/ 2700ns
load/store 350/300ns

Posledično: < 3MFLOPS/PE x 64
teoretično = 180MFLOPS
dejansko = 15MFLOPS

Primeri kaj se zgodi, če ljudje nekaj spregledajo…

program čas rač. celoten čas
I4TRES 10800s 22100s
2D-TRANSONIC 1110s 2000s
SAR 28s 52s

Problem je bil prepočasen V/I (prenosi v in iz pomnilnika), prehitro računal.

Zgled: Connection Machine 2

Connection Machine 2 (1987), naredili več kot 50, podjetje TCM (Thinking Machines Corporation). Ideja je bila naredit računalnik, ki je samo “number cruncher”, a uporaben za reševanje različnih problemov.

• \(2^{16}\) 1-bitnih procesorjev
• glavni pomnilnik imenovan Nexus
• 4 ali več gostečih (front-end) računalnikov, ki pripravlja stvari preden jih da v delu
• \(4\) kvadrantov, vsak s \(2^{14} = 16384\) procesorji, povezani z Nexus
• poseben V/I sistem z 1 do 8 “data vaults” (narejen iz diskov), da lahko podatke dovolj hitro prebere

2^4 = 16 1-bitnih procesorjev/plošči = 1 vozlišče
2^{16}/24 = 2^{12}, 12-hiperkocka
2 x 16 imamo 32-bitna enota za operacije v plavajoči vejici
2^11 32-bitnih operacij (na koncu uporabljalo za to, “number crunching”)
teoretična zmogljivost = 20GFLOPS

Vsi paralelni računalniki so za paralelne probleme, ne dobri za vse.

Prevlada MIMD

Po leti ~1990 so SIMD računalniki izginili, a zakaj?

1. Razvoj posebnih elementov za dano arhitekturo, saj je vsak SIMD je narejen drugače.
2. Razširljivost (scalability), kjer uporabnik želi velikost svojega računalnika prilagajati problemu, ki ga rešuje.
3. Razvoj tehnologije, saj ko so splošno namenski procesorji (off-the-shelf componenets) postali tako zmogljivi kot posebej narejeni in se ni več izplačalo delati SIMD.

Računalniku nič ne škodi, če deluje na MIMD način, le bolj splošen je. Tudi pri MIMD srečamo shared in distributed memory.

Problemi, ki se rešujejo običajno še vedno izkoriščajo operandno paralelnost, torej kot SIMD, a zmorejo tudi več.

Pregled

Date: 2014-03-17

• SISD
• Superskalarni
• Tomasulo algoritem
• Vektorski
• SIMD

MIMD računalniki

Zakaj so izginili SIMD?

1. Tehnološki razvoj
   • po letu ~1990 so “standardni” (off-the-shelf) procesorji postali dovolj zmogljivi.
2. Razširljivost SIMD je slaba
   • povečevanje zmogljivosti z dodajanjem procesorjev
   • povečanje zakasnitev (latence)
   • povečevanje cene
   • fizična velikost

Osnovni vrsti MIMD:

1. Skupen pomnilniški prostor
   • tesno sklopljen sistem
   • shared memory
   • UMA (uniform memory access)
   • vsak procesor \(P_i\) ima svoj predpomnilnik \(C_i\), ki so povezani v skupno povezovalno mrežo, le-ta pa na pomnilnik \(M_i\)
2. Več pomnilniških prostorov
   • rahlo sklopljen sistem
   • message passing
   • distributed memory
   • NUMA (non-uniform memory access)
   • vsaj procesor \(P_i\) ima svoj predpomnilnik \(C_i\) in pomnilnik \(M_i\), več pomnilniških prostorov, ki so šele potem povezani v povezovalno mrežo

Zgled: Tianhe-2

Lestvica TOP500 (teoretična zmogljivost):

2010 Tianhe-1A 4,7 PFLOPS 4,1 MW debelo drevo
2011 K computer 11,3 PFLOPS 12,6 MW “6D” torus (3D + dodatki)
2012 Titan-Cray XK7 27,1 PFLOPS 8,3 MW 3D torus
2013 Tianhe-2 54,9 PFLOPS 17,8 MW debelo drevo (+7 MW hlajenje)

Zgradba:

• plošča (board):
  • 2 modula:
    • CPM: 2x Ivy Bridge Xeon + 1x Xeon Phi)
    • APU (accelerated proc. unit): 5x Xeon Phi
    • mreža: 2x Gigabit LAN + TH-Express 2
  • 2 vozlišči/ploščo: 64 GB DRAM (Ivy Bridge) + 24 GB DRAM (Xeon Phi) = 88 GB/ploščo
• frame: 32 boards
• cabinet (rack): 4 frames = 128 boards
• computer: 125 cabinets (+ 13 za mrežo + 24 storage (diski))
• vodno hlajenje
• cena: ~500 M$

Heterogeni procesorji:

32000x Ivy Bridge Xeon E5-2692 2,2 GHz 12 jeder 211 GFLOPS/čip 115 W
48000x Xeon Phi 3151P 1,1 GHz 57 jeder 1003 GFLOPS/čip 270 W
Skupno jeder: \(32000 * 12 + 48000 * 57 = 3120000 jeder\) (procesorjev)
Teoretična hitrost: \(32000 * 0,211 + 48000 * 1,003 = 54896 PFLOPS\)

Diski: 12,4 PB, H2FS hierarhija

Mreža: debelo drevo

Primerjava: Grid/cloud computing

Folding@home 2011 6 PFLOPS
Folding@home 2013 12 PFLOPS
SETI@home 2013 15,4 PFLOPS
BOINC 2013 9,2 PFLOPS
Bitcoin 2014 414,5 EFLOPS

Majhna količina/potreba medprocesorske komunikacije, a takšnih primerov je zelo malo.

Cluster (gruča) je skupek istih računalniko povezanih skupaj.

Primerjava: GPU computing

Računanje na grafičnih procesorjih (MIMD). Prvotno specializirani za operacije za grafiko, dandanes imamo standard CUDA za lažjo uporabo.

Intelov odgovor na to je koprocesor npr. Xeon Phi, ki je združljiv in uporablja skoraj enake ukaze kot prej. Zmoljivost se drastično poveča: 16 FLOPS/cycle/core = 1003 GLOPS/core, 2x večja poraba, a hitrost 5x večja.

Kaj bo prevladalo? Koprocesorji ali GPU? Bomo videli.

Energetska učinkovitost

Tianhe-2 ~ \(3 GFLOPS/W\)

Lestvica Green500:

nov. 2013 4,503 GFLOPS/W 28 kW
           3,632 GFLOPS/W 52 kW
           3,518 GFLOPS/W 78 kW

Kako narediti ExaFlops (\(1000 PFLOPS\)) računalnik?

Problem za segrevanje je število preklopov, ker pri zniževanju napetosti najprej hitrost pade, pod \(0.7 V\) tranzistorji nehajo delati. Sodobni procesorji prilagajajo napetost/hitrost glede na obremenitev, temperaturo, in podobne faktorje.

V laboratorijih že imajo tranzistorje na drugačnih osnovah (\(0.3 V\)), a daleč od produkcije.

Podatkovno pretokovni računalniki (dataflow)

Obravnavali smo von Neumannove računalnike na katerih so od leta 1945 zasnovani vsi računalniki. Von Neumannov model je ukazno pretokovni (control flow) (strogo zaporedje: prevzem ukaza, izvršitev ukaza). Operand je točno določen z naslovom (oz. virtualnim naslovom).

Podatkovno pretokovni uporablja popolnoma drugačen pristop (ideja ~1950-ih, več pogovarjali v obdobju ~1960-1980). Problem lahko predstavimo kot graf operacij, npr:

\[ a = (b + 1) * (b - c) \]

1. operacijski paket
2. podatkovni žeton (token)

\[ \gamma: + (b) (1) \beta/1 \alpha: - (b) (c) \beta/2 \beta: * (\beta/1) (\beta/2) \delta/1=a \]

Podatkovni žetoni gredo v operacijske pakete na ustrezna mesta, njihov rezultati gredo naprej na ustrezna mesta v druge operacijske pakete.

Delovanje:

1. Data driven: operacija se izvrši, ko so prisotni vsi vhodni podatki
2. Demand driven: enako kot 1. + operacijski paket potrebuje rezultat

Operacije:

• funkcija \(f\), (krog, več vhodov, en izhod)
• odločitev, (diamant, več vhodov, en izhod)
• vrata \(T\), spusti skozi, ko true, (krog s puščico, en vhod, en izhod)
• preklop \(T/F\), if stavek izbere med dvema vhodoma, (krog s puščico, dva vhoda, en izhod)
• preklop \(T/F\), if stavek izbere izhod, (krog s puščico, en vhod, dva izhoda)

Tipi:

1. statični podatkovno pretokovni rač. (1974 J. Damis):
   • na loku grafa je lahko največ 1 žeton
   • operacija se izvrši, če so prisotni vhodni operandi + prazen lok
2. dinamični podatkovno pretokovni rač. (1982 Manchester; 1983 Amind, MIT:
   • na loku grafa je lahko več žetonov
   • žetoni morajo biti oštevilčeni (obarvani)

Napake glede naslovov se ne morejo zgoditi, saj pojem naslova ne obstaja in ga po pomoti ni možno pokvariti (eg. stack overflow). V grafih nobene omejitve glede zaporednosti.

Kako naredimo takšen računalnik? (podobno je paketni mreži)

• gosteči računalnik (zaradi lažje implementacije)
• V/I stikalo nadzira gosteči računalnik
• vsakemu podatku se glede na vrsto priredi podatkovni žeton
• primerjalna enota vsebuje program oz. operacijske pakete, čaka na ustrezne žetone
• operacijski paketi z vsemi žetoni nato potujejo v pomnilnik oz. čakalno vrsto
• le-ti gredo nato v množico procesorjev iz katere pridejo žetoni rezultatov, ki spet po potrebi zaokrožijo

Problemi:

• zmogljivost primerjalne enote, število primerjalnikov v malo večjem asociativnem predpomnilniku zelo naraste
• paketna mreža ima enake probleme kot vse mreže, so lahko ozke mreže in procesorji lahko čakajo
• velika “poraba” pomnilnika, vsaka spremenljivka ima lahko v nekem trenutku veliko število žetonov (npr. operacije z matrikami, kjer lahko iz ene vrednosti nastane več)

Takih računalnikov na trgu ni, razen za posebne namene. Kljub temu, da je ideja sicer zanimiva in nekaterih težav z njimi ni (stroge zaporednosti, segmentation fault), se niso obnesli, saj niso bolj zmogljivi.

Ostali:

• analogni računalniki (z žicami, 1% natančnost), hibridni (lažje programirat)
• nevronske mreže (pripravijo na PCju, lahko specializirana vezja), primerni za določene primere (npr. razpoznavanje obrazov)